Getting Started with SBC

What is SBC?

SBC stands for “simulation-based calibration” and it is a tool to validate statistical models and/or algorithms fitting those models. In SBC we are given a statistical model, a method to generate draws from the prior predictive distribution (i.e. generate simulated datasets that match the model’s priors + likelihood) and an algorithm that fits the model to data.

The rough sketch of SBC is that we simulate some datasets and then for each simulated dataset:

Fit the model and obtain \(D\) independent draws from the posterior.
For each variable of interest, take the rank of the simulated value within the posterior draws
- Where rank is defined as the number of draws < simulated value

It can be shown that if model matched the generator and algorithm works correctly, then for each variable, the ranks obtained in SBC should be uniformly distributed between \(0\) and \(D\). This corresponds quite directly to claims like “the posterior 84% credible interval should contain the simulated value in 84% of simulations”, the rank uniformity represents this claim for all interval widths at once. The theory of SBC is fully described in Modrák et al. which builds upon Talts et al.

This opens two principal use-cases of SBC:

We have an algorithm that we trust is correct and a generator and and we want to check that we correctly implemented our Bayesian model
We have a generator and a model we trust and we want to check whether a given algorithm correctly computes the posterior.

In any case, a failure of SBC only tells us that at least one of the three pillars of our inference (generator/model/algorithm) is mismatched to others.

In the context of larger Bayesian workflow (as discussed e.g. in Bayesian Workflow by Gelman et al. or Towards A Principled Bayesian Workflow by Betancourt), SBC can be used to validate the implementation of a model/algorithm, which is just one of many things to check if one needs a robust analysis. In particular, SBC does not use any real data and thus cannot tell you anything about potential mismatch between your model and the actual data you plan to analyze. However, this is in some sense an advantage: if our model fails (e.g. we have convergence problems) on real data, we don’t know whether the problem is a bug in our model or a mismatch between the model and the data. If we simulate data exactly as the model assumes, any problem has to be a bug. Additionally, we can use SBC to better understand whether the data we plan to collect are actually capable of answering the questions we have.

This vignette will demonstrate how the basic package interface can be used to run simulations, calculate ranks and investigate calibration.

Aims of the package

The SBC package aims to provide a richer and more usable alternative to rstan::sbc(). The main design goals is to make it easy to incorporate SBC in your everyday modelling workflow. To this end:

No changes to your model are needed to test it with SBC.
Once you have your model and code to simulate data ready, it is easy to gradually move from 1 simulation to check your model does not crash to 1000 simulations that can resolve even small inaccuracies.

We intentionally do not focus on mechanisms that would let you automatically construct a simulator just from your model: if we did that, any bugs in your model would automatically carry over to the simulator and the SBC would only check that the algorithm works. Instead we believe it is good practice to implement the simulator in the most easy way possible while altering aspects of the implementation that should not matter (e.g. for loops vs. matrix multiplication). The best solution would be to have one person write the simulator and a different person the model (though that would often be impractical). This way you get two independent pieces of code that should correspond to the same data generating process and it becomes less likely that there is the same mistake in both versions. A mistake that is in just one version can then be (at least in principle) caught by SBC.

This is actually a well known pattern in software safety: critical components in airplanes are required to have two completely independent implementations of the same software (or even hardware) and the system checks that both produce the same output for the same input. Similarly, pharmaceutical companies analyzing drug trials are required to have the data analysis pipeline written by two separate teams and the results of both must match (this is not required for academic trials - who would need safety there, right?). The main reason this method is used relatively rarely is that implementing the same thing twice is costly. But statistical models are usually relatively small pieces of code and the added cost of the second implementation (the generator) thus tends to very small.

Naming

To avoid confusion the package and the docs tries to consistently give the same meaning to the following potentially ambiguous words:

variable All quantities of interest for SBC - this includes both parameters that are directly estimated by the model and quantities derived from those parameters.
draws are assumed to come from either a single realized posterior distribution of a fitted model or the prior distribution of the model. The number of draws ( n_draws) is the number of posterior draws produced by fitting the model.
simulation / sim a set of simulated values for all variables and the accompanying generated data. I.e. the number of simulations (n_sims) is the number of times an individual model is fitted
fit represents the result of fitting a single simulation

Overview of the Architecture

Overview of the package structure

To perform SBC, one needs to first generate simulated datasets and then fit the model to those simulations. The SBC_datasets object holds the simulated prior and data draws. SBC_datasets objects can be created directly by the user, but it is often easier to use one of provided Generator implementations that let you e.g. wrap a function that returns the variables and observed data for a single simulation or use a brms specification to generate draws corresponding to a given brms model.

The other big part of the process is a backend. The SBC package uses a backend object to actually fit the model to the simulated data and generate posterior draws. In short, backend bundles together the algorithm in which inference is run (cmdstanr, rstan, brms, jags, etc.), the model, and additional platform-specific inference parameters which are necessary to run inference for the model-platform combination (e.g. number of iterations, initial values, …). In other words backend is a function that takes data as its only input and provides posterior draws.

Once we have a backend and an SBC_datasets instance, we can call compute_SBC to actually perform the SBC. The resulting object can then be passed to various plotting and summarising functions to let us easily learn if our model works as expected.

Simple Poisson Regression

In this vignette we will demonstrate how the interface is used with a simple poisson model. First we’ll setup and configure our environment.

library(SBC)
library(ggplot2)

use_cmdstanr <- getOption("SBC.vignettes_cmdstanr", TRUE) # Set to false to use rstan instead

if(use_cmdstanr) {
  library(cmdstanr)
} else {
  library(rstan)
  rstan_options(auto_write = TRUE)
}

options(mc.cores = parallel::detectCores())

# Enabling parallel processing via future
library(future)
plan(multisession)

# The fits are very fast,
# so we force a minimum chunk size to reduce overhead of
# paralellization and decrease computation time.
options(SBC.min_chunk_size = 5)

# Setup caching of results
if(use_cmdstanr) {
  cache_dir <- "./_basic_usage_SBC_cache"
} else {
  cache_dir <- "./_basic_usage_rstan_SBC_cache"
}
if(!dir.exists(cache_dir)) {
  dir.create(cache_dir)
}

theme_set(theme_minimal())

# Run this _in the console_ to report progress for all computations to report progress for all computations
# see https://progressr.futureverse.org/ for more options
progressr::handlers(global = TRUE)

Model Setup

We will be running SBC against a model that defines y ~ Poisson(lambda), where lambda ~ Gamma(15, 5). We will use the following Stan model:

cat(readLines("stan/poisson.stan"), sep = "\n")

data{
  int N;
  array[N] int y;
}
parameters{
  real<lower = 0> lambda;
}
model{
  lambda ~ gamma(15, 5);
  y ~ poisson(lambda);
}

if(use_cmdstanr) {
  cmdstan_model <- cmdstanr::cmdstan_model("stan/poisson.stan")
} else {
  rstan_model <- rstan::stan_model("stan/poisson.stan")
}

Generator

Once we have defined the model, we can create a generator function which will generate prior and data draws:

# A generator function should return a named list containing elements "variables" and "generated"

poisson_generator_single <- function(N){  # N is the number of data points we are generating
  lambda <- rgamma(n = 1, shape = 15, rate = 5)
  y <- rpois(n = N, lambda = lambda)
  list(
    variables = list(
      lambda = lambda
    ),
    generated = list(
      N = N,
      y = y
    )
  )
}

As you can see, the generator returns a named list containing random draws from the prior and generated data realized from the prior draws - the data are already in the format expected by Stan.

Create `SBC_datasets` from generator

SBC provides helper functions SBC_generator_function and generate_datasets which takes a generator function and calls it repeatedly to create a valid SBC_datasets object.

set.seed(54882235)
n_sims <- 100  # Number of SBC iterations to run

poisson_generator <- SBC_generator_function(poisson_generator_single, N = 40)
poisson_dataset <- generate_datasets(
  poisson_generator, 
  n_sims)

Defining backend

Once we have the model compiled we’ll create a backend object from the model. SBC includes pre-defined backend objects for HMC sampling with cmdstan and rstan. In addition, it also provides generator function and backend for brms based models.

Note that you can create your own backend if you wish to use a different sampling/optimization platform, such as variational inference or JAGS.

Here we’ll just use the pre-defined cmdstan backend, in which we pass our compiled model and any additional arguments we would like to pass over to the sampling method:

if(use_cmdstanr) {
  poisson_backend <- SBC_backend_cmdstan_sample(
    cmdstan_model, iter_warmup = 1000, iter_sampling = 1000, chains = 2)
} else {
  poisson_backend <- SBC_backend_rstan_sample(
    rstan_model, iter = 2000, warmup = 1000, chains = 2)  
}

Computing Ranks

we can then use compute_SBC to fit our simulations with the backend:

results <- compute_SBC(poisson_dataset, poisson_backend, 
                    cache_mode = "results", 
                    cache_location = file.path(cache_dir, "results"))

## Results loaded from cache file 'results'

##  - 96 (96%) fits had steps rejected. Maximum number of steps rejected was 3.

##  - 1 (1%) fits had maximum Rhat > 1.01. Maximum Rhat was 1.011.

## Not all diagnostics are OK.
## You can learn more by inspecting $default_diagnostics, $backend_diagnostics 
## and/or investigating $outputs/$messages/$warnings for detailed output from the backend.

Here we also use the caching feature to avoid recomputing the fits when recompiling this vignette. In practice, caching is not necessary but is often useful.

Viewing Results

We can now inspect the results to see if there were any errors and check individual stats:

dplyr::select(results$stats, sim_id:ess_tail) # Hiding some less useful statistics for clarity

##     sim_id variable simulated_value rank      z_score     mean        sd
## 1        1   lambda        1.441812   13 -1.501694087 1.725853 0.1891470
## 2        2   lambda        2.991399   86 -0.188887934 3.039493 0.2546170
## 3        3   lambda        2.505585   49 -0.698130727 2.680618 0.2507169
## 4        4   lambda        2.863184   54 -0.683807732 3.039353 0.2576293
## 5        5   lambda        2.972115  170  1.158010949 2.679651 0.2525576
## 6        6   lambda        2.544888  160  0.847982761 2.351286 0.2283092
## 7        7   lambda        2.646566   19 -1.435321388 3.021170 0.2609897
## 8        8   lambda        2.988570  135  0.286440559 2.913205 0.2631121
## 9        9   lambda        2.554855   18 -1.318712834 2.881521 0.2477156
## 10      10   lambda        1.725117    8 -1.472702333 2.034624 0.2101624
## 11      11   lambda        1.983277   78 -0.326961775 2.051754 0.2094347
## 12      12   lambda        3.173095  113  0.133791039 3.137776 0.2639852
## 13      13   lambda        3.205621  198  2.500128948 2.579017 0.2506287
## 14      14   lambda        3.612096  173  1.063996007 3.328464 0.2665724
## 15      15   lambda        2.808949  168  1.052663180 2.558607 0.2378178
## 16      16   lambda        2.070563   39 -0.737282660 2.233066 0.2204075
## 17      17   lambda        2.779688  175  1.017966062 2.532166 0.2431538
## 18      18   lambda        2.925609   57 -0.396791487 3.026416 0.2540549
## 19      19   lambda        2.750356  163  0.771996557 2.572147 0.2308416
## 20      20   lambda        3.106723   24 -1.292459173 3.452304 0.2673831
## 21      21   lambda        3.412007  178  1.162445949 3.102721 0.2660655
## 22      22   lambda        3.616894  134  0.386958384 3.510529 0.2748741
## 23      23   lambda        2.294084  181  1.150986026 2.049403 0.2125836
## 24      24   lambda        2.116142   54 -0.659973413 2.264633 0.2249960
## 25      25   lambda        2.249235   70 -0.636187617 2.394124 0.2277471
## 26      26   lambda        2.687811  142  0.651437515 2.531350 0.2401782
## 27      27   lambda        1.752253   11 -1.655833148 2.108951 0.2154195
## 28      28   lambda        1.824980  148  0.627335305 1.707876 0.1866686
## 29      29   lambda        3.046774  119  0.192941536 2.997602 0.2548539
## 30      30   lambda        2.545681  128  0.392452970 2.453543 0.2347743
## 31      31   lambda        2.547563   39 -0.918523211 2.767952 0.2399379
## 32      32   lambda        2.530286  110 -0.031976145 2.537975 0.2404466
## 33      33   lambda        3.488554  198  3.043916402 2.715768 0.2538789
## 34      34   lambda        4.202627  196  2.496287925 3.500742 0.2811716
## 35      35   lambda        2.202380  119  0.291485119 2.139633 0.2152660
## 36      36   lambda        2.776523   48 -0.627618807 2.936541 0.2549593
## 37      37   lambda        4.745755  151  0.596548268 4.556775 0.3167897
## 38      38   lambda        2.926568  178  1.158966774 2.644426 0.2434423
## 39      39   lambda        3.207927   83 -0.282692174 3.283654 0.2678755
## 40      40   lambda        2.050516  118  0.221334899 2.004112 0.2096562
## 41      41   lambda        2.949112  101 -0.088324032 2.971600 0.2546051
## 42      42   lambda        2.027079   97 -0.141357389 2.056636 0.2090940
## 43      43   lambda        3.109239  131  0.543625486 2.969326 0.2573700
## 44      44   lambda        3.121440  182  1.361716605 2.781752 0.2494558
## 45      45   lambda        4.243259  132  0.571397898 4.076947 0.2910609
## 46      46   lambda        2.744712  196  1.725694537 2.366205 0.2193362
## 47      47   lambda        4.132018  199  3.505528124 3.235931 0.2556211
## 48      48   lambda        1.557847   24 -1.230794572 1.788938 0.1877573
## 49      49   lambda        2.532101   84 -0.168158392 2.572108 0.2379113
## 50      50   lambda        2.964897  146  0.560512317 2.824785 0.2499719
## 51      51   lambda        3.681536  161  0.798744318 3.466995 0.2685976
## 52      52   lambda        3.144808  119  0.193597909 3.094643 0.2591180
## 53      53   lambda        3.887949  163  0.889580436 3.644047 0.2741762
## 54      54   lambda        3.196185  161  1.013230448 2.935216 0.2575613
## 55      55   lambda        2.995181  146  0.465233319 2.874634 0.2591108
## 56      56   lambda        2.356170   60 -0.463845458 2.464982 0.2345870
## 57      57   lambda        2.292702    2 -2.002135379 2.798191 0.2524748
## 58      58   lambda        3.566893    6 -1.950857748 4.151991 0.2999184
## 59      59   lambda        3.373654   14 -1.529297940 3.820671 0.2923023
## 60      60   lambda        4.211833  117  0.285687477 4.126979 0.2970168
## 61      61   lambda        2.249955   75 -0.424211895 2.344588 0.2230796
## 62      62   lambda        1.990641  169  0.907181565 1.816890 0.1915280
## 63      63   lambda        2.588078   45 -0.824126352 2.795250 0.2513843
## 64      64   lambda        1.916143   36 -0.858133907 2.098943 0.2130208
## 65      65   lambda        1.432994   23 -1.283940633 1.675846 0.1891459
## 66      66   lambda        4.605845  105  0.221880843 4.535067 0.3189899
## 67      67   lambda        1.971748  177  1.403854791 1.702277 0.1919511
## 68      68   lambda        2.573467  143  0.714389461 2.413336 0.2241500
## 69      69   lambda        3.574121   56 -0.618650521 3.753693 0.2902633
## 70      70   lambda        3.301493   11 -1.539104657 3.743910 0.2874509
## 71      71   lambda        2.865513  116  0.139942995 2.829747 0.2555786
## 72      72   lambda        2.675924  125  0.270666958 2.607764 0.2518199
## 73      73   lambda        2.700097   70 -0.239242926 2.760478 0.2523851
## 74      74   lambda        2.287127   10 -1.741721959 2.711650 0.2437374
## 75      75   lambda        3.466282  189  1.907325909 2.959903 0.2654916
## 76      76   lambda        2.780579   26 -1.071945933 3.069806 0.2698142
## 77      77   lambda        2.711286  121  0.298966076 2.639061 0.2415853
## 78      78   lambda        3.704305  176  1.142914504 3.408947 0.2584253
## 79      79   lambda        2.137092   21 -1.244406493 2.419204 0.2267038
## 80      80   lambda        3.885904   71 -0.473028614 4.028637 0.3017438
## 81      81   lambda        2.975582  153  0.520945954 2.841588 0.2572129
## 82      82   lambda        2.555879  197  2.525528624 2.034529 0.2064320
## 83      83   lambda        1.714758   11 -1.623054828 2.063051 0.2145911
## 84      84   lambda        2.939516  148  0.731297356 2.755810 0.2512051
## 85      85   lambda        2.012372   78 -0.289527799 2.072870 0.2089526
## 86      86   lambda        2.042660  109  0.131531033 2.015090 0.2096073
## 87      87   lambda        2.831330  105 -0.001604659 2.831756 0.2656496
## 88      88   lambda        4.146054  104 -0.009810902 4.149050 0.3054299
## 89      89   lambda        4.269022  188  1.393655334 3.847800 0.3022428
## 90      90   lambda        2.674868  169  0.934662376 2.457930 0.2321039
## 91      91   lambda        2.638067   53 -0.597978687 2.789752 0.2536641
## 92      92   lambda        3.491849  160  0.834545540 3.270545 0.2651788
## 93      93   lambda        2.534526   66 -0.438036655 2.642202 0.2458164
## 94      94   lambda        3.659232  136  0.426876388 3.542485 0.2734903
## 95      95   lambda        2.892749   66 -0.522133631 3.030465 0.2637561
## 96      96   lambda        3.481138  121  0.301675259 3.399947 0.2691328
## 97      97   lambda        3.280706   68 -0.395256190 3.389850 0.2761353
## 98      98   lambda        2.830662  175  1.263187438 2.530392 0.2377085
## 99      99   lambda        4.738485   95 -0.139809747 4.783307 0.3205959
## 100    100   lambda        3.067411   66 -0.481830474 3.197087 0.2691335
##           q5   median      q95      rhat ess_bulk  ess_tail
## 1   1.425542 1.725310 2.051346 1.0011869 660.0295  715.1319
## 2   2.633600 3.031315 3.471290 0.9997378 723.2247  818.7563
## 3   2.286277 2.668550 3.106196 0.9995790 653.5429  960.0598
## 4   2.635808 3.033580 3.470293 1.0002172 819.4936 1003.8764
## 5   2.278813 2.664300 3.119555 1.0016487 737.6552  984.2296
## 6   1.996707 2.341710 2.742270 0.9997896 842.6717 1090.9653
## 7   2.600472 3.017635 3.462150 1.0004873 760.8959  739.4559
## 8   2.507262 2.895780 3.362985 1.0006535 533.3517  856.9942
## 9   2.492170 2.873655 3.309812 1.0052057 744.3574 1074.7049
## 10  1.713043 2.031755 2.390874 1.0054013 679.3340 1040.8612
## 11  1.724270 2.042795 2.403703 1.0010527 815.0111  973.0837
## 12  2.716921 3.130805 3.574737 1.0053059 651.7761 1039.7132
## 13  2.183970 2.561650 3.017141 1.0026517 703.2212  811.6780
## 14  2.888450 3.321515 3.765640 1.0026125 750.3075  840.0322
## 15  2.175213 2.553435 2.969768 0.9998641 730.6925 1259.4481
## 16  1.879628 2.222870 2.607362 1.0047340 516.6965 1040.3195
## 17  2.144321 2.525805 2.946923 0.9995265 715.9406  920.1079
## 18  2.623396 3.009830 3.461660 1.0012452 697.5614 1029.8202
## 19  2.211069 2.568220 2.962087 1.0003297 751.0762 1065.1954
## 20  3.005747 3.452150 3.900292 1.0000789 993.2648  935.2418
## 21  2.704091 3.080630 3.572188 1.0001495 681.6749  948.6171
## 22  3.075141 3.505210 3.979986 1.0003745 667.7095  758.5672
## 23  1.709310 2.044630 2.428970 1.0001475 796.9757 1075.3850
## 24  1.903339 2.252245 2.657170 1.0087929 708.9603 1041.2990
## 25  2.026301 2.390120 2.775346 1.0029391 646.7598 1209.1364
## 26  2.155518 2.522120 2.937612 1.0001582 715.5761  890.9293
## 27  1.771833 2.105525 2.461035 0.9998778 767.3054 1031.3733
## 28  1.409583 1.703375 2.025194 1.0006236 880.7755 1026.9417
## 29  2.588206 2.989975 3.442743 1.0006011 905.0299  939.5602
## 30  2.082984 2.448860 2.863097 0.9999949 658.9626 1112.4987
## 31  2.391096 2.757415 3.182740 1.0000495 921.9282 1102.0187
## 32  2.160176 2.523790 2.948411 0.9999317 787.3817 1127.8414
## 33  2.305504 2.709085 3.144192 0.9997342 842.8924  798.3485
## 34  3.060178 3.482410 3.988796 0.9998837 806.4903 1101.2251
## 35  1.804955 2.131940 2.513515 0.9998412 768.2363 1065.1438
## 36  2.527412 2.929765 3.358909 1.0006236 788.5764  878.1683
## 37  4.059522 4.545045 5.090742 1.0013545 718.6773  977.0057
## 38  2.247564 2.639940 3.055171 1.0003029 667.0379  954.3288
## 39  2.859915 3.265925 3.749442 1.0113134 736.0217  919.8987
## 40  1.669045 2.000295 2.345767 1.0085661 851.1195 1009.1286
## 41  2.570919 2.960900 3.406436 1.0035349 798.4497 1012.2082
## 42  1.707909 2.052685 2.410390 1.0021600 924.9461  805.3713
## 43  2.565836 2.960190 3.406040 1.0010983 637.5778  997.6310
## 44  2.378691 2.778855 3.204051 0.9995515 700.9183  950.1423
## 45  3.606645 4.070870 4.571690 1.0048858 809.0206  967.6233
## 46  2.016641 2.352885 2.737163 1.0007081 719.9356  922.7823
## 47  2.840629 3.225550 3.671694 0.9995151 864.0128 1018.6007
## 48  1.499041 1.784640 2.105972 1.0002198 827.7344  940.7343
## 49  2.190192 2.568805 2.965094 1.0006513 712.4777  690.9827
## 50  2.429369 2.813880 3.251746 0.9999529 800.9823  994.8016
## 51  3.028606 3.459785 3.915139 1.0039387 643.1534  931.8337
## 52  2.685204 3.092625 3.532625 1.0007379 727.3670  897.1089
## 53  3.195210 3.636965 4.088961 1.0013633 720.6847  982.5962
## 54  2.526422 2.919155 3.370417 1.0008260 769.3383  947.2193
## 55  2.460466 2.856135 3.311713 1.0005429 940.9927  877.1722
## 56  2.088611 2.460160 2.868999 1.0034291 739.7487  755.3741
## 57  2.394655 2.794805 3.216873 1.0013400 745.4077 1204.6245
## 58  3.655847 4.146495 4.671717 0.9997149 791.2195  821.9506
## 59  3.338982 3.819130 4.297463 1.0004572 773.0375  822.5117
## 60  3.659943 4.117970 4.621887 1.0012200 743.4275  920.1718
## 61  1.997918 2.337445 2.725312 1.0015517 800.5474  992.6161
## 62  1.509629 1.814020 2.147109 1.0016081 954.9923  855.9785
## 63  2.404316 2.786740 3.224042 1.0001407 588.4572  879.4026
## 64  1.760494 2.092000 2.456535 1.0001785 545.6342 1018.6007
## 65  1.373037 1.667420 1.997669 1.0043744 791.7959  919.3614
## 66  4.018374 4.530270 5.064019 1.0008219 638.0565  872.9338
## 67  1.400203 1.691045 2.034384 0.9997568 842.8434  995.9205
## 68  2.053593 2.414575 2.795053 1.0037357 763.3728 1005.0143
## 69  3.269985 3.751370 4.242865 1.0037733 794.3672  853.1240
## 70  3.284205 3.736505 4.223986 1.0009122 670.6007  772.5784
## 71  2.427074 2.818530 3.261154 1.0009674 637.9633  852.9921
## 72  2.215489 2.595775 3.033569 1.0003754 773.7432 1075.7196
## 73  2.361864 2.751815 3.195270 0.9995269 668.6138  754.8831
## 74  2.318596 2.692930 3.117669 1.0005643 732.1138 1261.6604
## 75  2.527322 2.953010 3.403400 1.0045287 704.5385  851.0551
## 76  2.647189 3.058175 3.533150 1.0005898 648.3222  954.0315
## 77  2.253260 2.629410 3.045765 1.0010361 701.6761  882.7765
## 78  2.995416 3.402950 3.852020 1.0076472 839.9925 1056.1061
## 79  2.050113 2.420890 2.800033 1.0011415 846.4774  898.8490
## 80  3.538894 4.015595 4.545651 1.0005755 791.5733  943.3290
## 81  2.433290 2.836725 3.279304 0.9996790 632.0390 1077.6820
## 82  1.703770 2.030265 2.380612 0.9998971 875.5376 1182.7928
## 83  1.727612 2.053290 2.418300 1.0013763 826.5146 1087.3262
## 84  2.351135 2.753480 3.172129 1.0000357 644.1129  935.7840
## 85  1.745923 2.068240 2.430044 1.0001230 804.6764 1258.8233
## 86  1.679003 2.008805 2.366873 0.9998991 761.3000  901.9266
## 87  2.421136 2.818110 3.292978 1.0026520 686.2053  903.2702
## 88  3.657878 4.137180 4.668840 0.9995274 676.0670 1068.8565
## 89  3.352123 3.836910 4.349346 1.0008308 739.0588  798.1038
## 90  2.067192 2.457640 2.856483 1.0006057 668.7194  667.8999
## 91  2.389628 2.779020 3.232007 1.0007516 608.3822  773.1341
## 92  2.854354 3.259910 3.727297 0.9996340 791.2937 1058.0783
## 93  2.249837 2.634340 3.073669 1.0006354 932.8111  859.4093
## 94  3.101970 3.538840 4.001970 1.0003342 651.7645  950.3954
## 95  2.607559 3.018795 3.492941 1.0000664 680.9596  792.3254
## 96  2.971889 3.388770 3.863469 1.0054110 713.5742 1032.3749
## 97  2.951304 3.381640 3.856842 0.9998179 764.5710 1138.7384
## 98  2.165190 2.520520 2.944158 1.0024905 711.3937  952.3345
## 99  4.254724 4.779785 5.336192 1.0013898 635.3145  817.4980
## 100 2.764843 3.194175 3.652710 1.0005225 627.0584  700.2526

Plots

And finally, we can plot the rank distribution to check if the ranks are uniformly distributed. We can check the rank histogram and ECDF plots (see vignette("rank_visualizations") for description of the plots):

plot_rank_hist(results)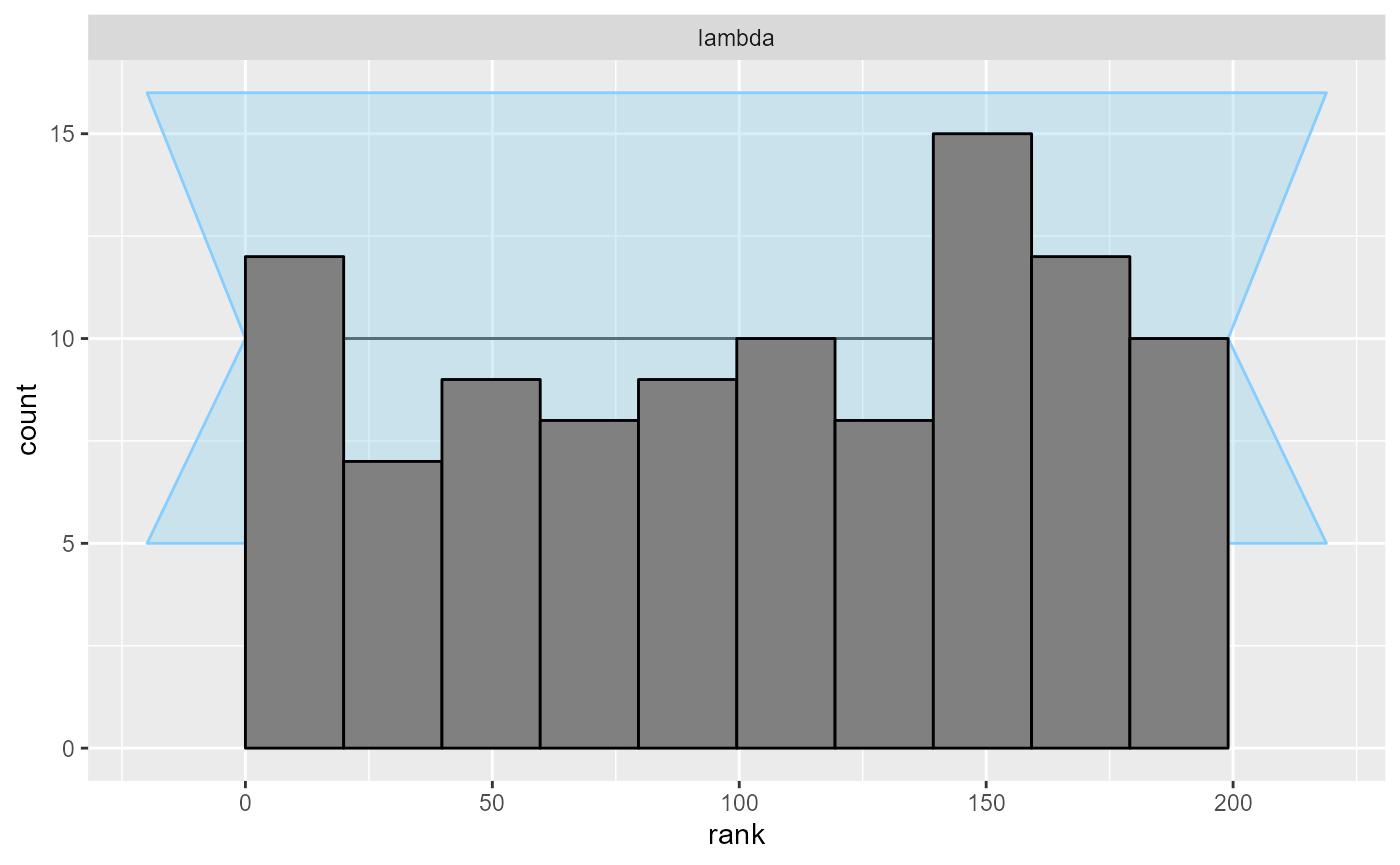

plot_ecdf(results)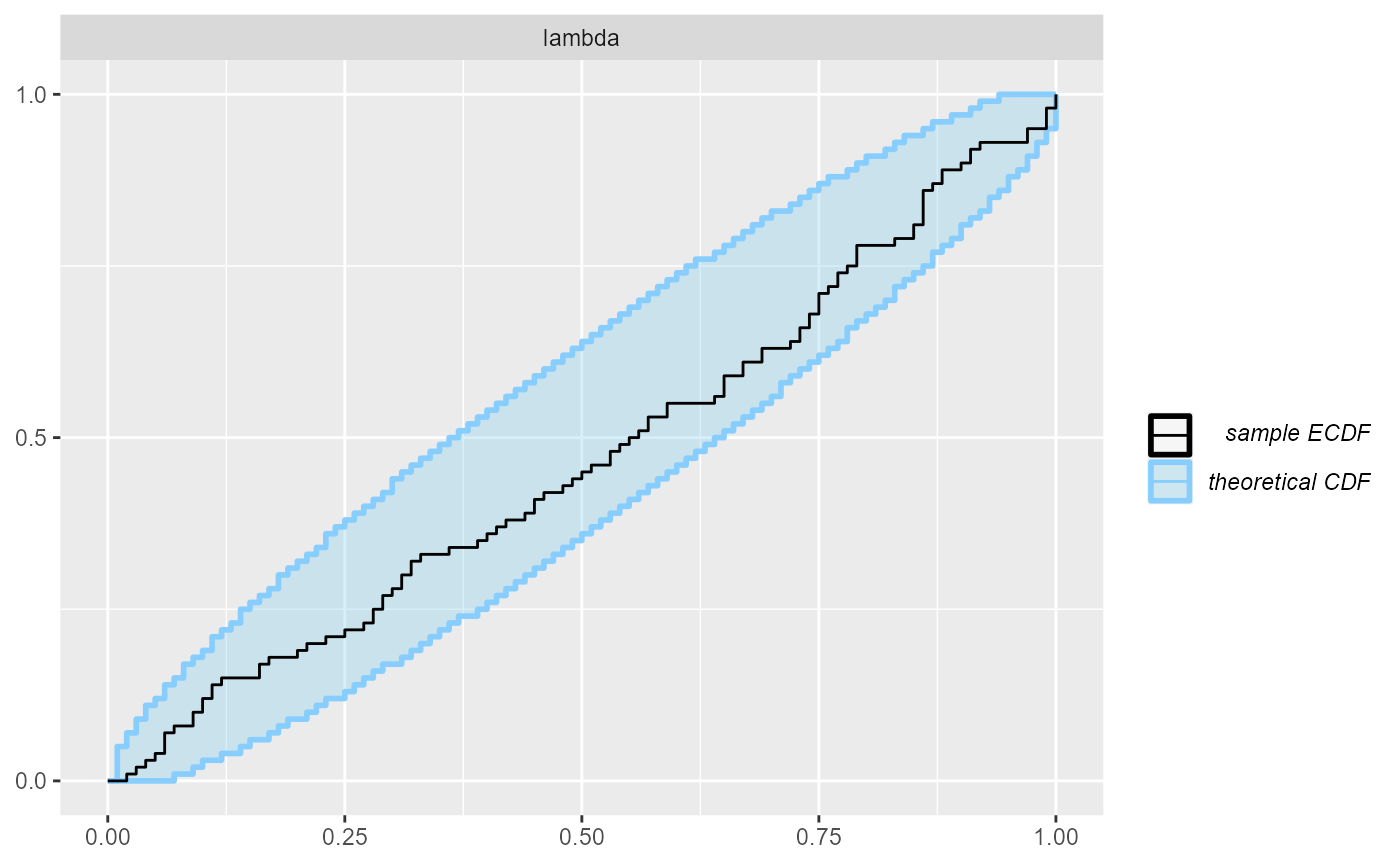

plot_ecdf_diff(results)

Since our simulator and model do match and Stan works well, we see that the plots don’t show any violation.

Is SBC frequentist?

A bit of philosophy at the end - SBC is designed to test Bayesian models and/or algorithms, but it fits very well with standard frequentist ideas (and there is no shame about this). In fact, SBC can be understood as a very pure form of hypothesis testing as the “null hypothesis” that the ranks are uniformly distributed is completely well specified, can (beyond numerical error) actually hold exactly and we are conducting the test against a hypothesis of interest. SBC thus lets us follow a simple naive-Popperian way of thinking: we try hard to disprove a hypothesis (that our model + algorithm + generator is correct) and when we fail to disprove it, we can consider the hypothesis corroborated to the extent our test was severe. This is unlike many scientific applications of hypothesis testing where people use a rejection of the null hypothesis as evidence for alternative (which is usually not warranted).

We currently can’t provide a good theoretical understanding of the severity of a given SBC test, but obviously the more iterations and the narrower the confidence bands of the ecdf and ecdf_diff plots, the more severe the test. One can also use empirical_coverage() and plot_coverage() functions to investigate the extent of miscalibration that we cannot rule out given our results so far.

Alternatively, one can somewhat sidestep the discussions about philosophy of statistics and understand SBC as a probabilistic unit test for your model. In this view, SBC tests a certain identity that we expect to hold if our system is implemented correctly, similarly how one could test an implementation of an arithmetical system by comparing the results of computing \((x + y)^2\) and \(x^2 + 2xy + y^2\) - any mismatch means the test failed.

Where to go next?

You may want to explore short examples showing how SBC can be used to diagnose bad parametrization or indexing bugs or you may want to read through a longer example of what we consider best practice in model-building workflow.

Alternatively, you might be interested in the limits of SBC — the types of problems that are hard / impossible to catch with SBC and what can we do to guard against those.

Acknowledgements

Development of this package was supported by ELIXIR CZ research infrastructure project (Ministry of Youth, Education and Sports of the Czech Republic, Grant No: LM2018131) including access to computing and storage facilities.

Hyunji Moon, Martin Modrák, Shinyoung Kim

2025-09-17

What is SBC?

Aims of the package

Naming

Overview of the Architecture

Simple Poisson Regression

Model Setup

Generator

Create `SBC_datasets` from generator

Defining backend

Computing Ranks

Viewing Results

Plots

Is SBC frequentist?

Where to go next?

Acknowledgements

Getting Started with SBC

Hyunji Moon, Martin Modrák, Shinyoung Kim

2025-09-17

What is SBC?

Aims of the package

Naming

Overview of the Architecture

Simple Poisson Regression

Model Setup

Generator

Create SBC_datasets from generator

Defining backend

Computing Ranks

Viewing Results

Plots

Is SBC frequentist?

Where to go next?

Acknowledgements

Create `SBC_datasets` from generator