Rejection sampling in simulations
Martin Modrák
2024-03-14
Source:vignettes/rejection_sampling.Rmd
rejection_sampling.RmdIn some cases, one may want to exclude extreme simulations from SBC (e.g. because those simulations create divergences). It is best to use prior predictive checks to examine your priors and change them to avoid extremes in the simulated data. In some cases, this may however be impractical/impossible to do via prior choice - one example are regression coefficients, where once we have many predictors, any independent prior that is not very strict will lead to unrealistic predictions. Joint priors are needed in such case, but those are not well understood and easy to use. See Paul Bürkner’s talk on SBC StanConnect for more context.
An alternative is to use rejection sampling i.e. we repeatedly generate a simulation and only accept it when it passes a certain condition we impose (e.g. that no observed count is larger than \(10^8\)). But does rejection sampling when generating simulations affect the validity of SBC?
It turns out that it does not as long as the rejection criterion only uses observed data and not the unobserved variables.
We’ll first walk through the math and then show examples of both OK and problematic rejection sampling.
The math
Let \(\mathtt{accept}(y)\) be the probability the the simulated data \(y\) is accepted. Note that \(\mathtt{accept}\) uses only data as input and would usually be a 0-1 function if you have a clear idea what a “bad” dataset looks like, but could be probabilistic if you’re relying on finicky diagnostics.
We define a variable \(a \sim \text{Bernoulli}(\mathtt{accept}(y))\). Given the parameter space \(\Theta\) and a specific \(\theta \in \Theta\), this implies a joint distribution \(\pi(\theta, y, a)\) that factorizes as \(\pi(\theta, y, a) = \pi(a|y)\pi(y | \theta)\pi(\theta)\). We can then look at the posterior conditional on accepting a dataset to see the claimed invariance:
\[ \begin{equation} \pi(\theta | y, a = 1) = \frac{\pi(a = 1 | y) \pi(y | \theta)\pi(\theta)}{\int_\Theta \mathrm{d}\tilde\theta \: \pi(a = 1 | y) \pi(y | \tilde\theta)\pi(\tilde\theta)} = \frac{\pi(y | \theta)\pi(\theta)}{\int_\Theta \mathrm{d}\tilde\theta \: \pi(y | \tilde\theta)\pi(\tilde\theta)} = \pi(\theta | y) \end{equation} \]
So whether we take rejection into account or not, the model will match the generating process. However, if \(\mathtt{accept}\) also depended on \(\theta\), it would no longer contribute a constant and we’ll get a mismatch between the generator and model.
Practical examples
So let’s see if that also happens in practice. Let’s setup our environment:
library(SBC)
use_cmdstanr <- getOption("SBC.vignettes_cmdstanr", TRUE) # Set to false to use rstan instead
if(use_cmdstanr) {
library(cmdstanr)
} else {
library(rstan)
rstan_options(auto_write = TRUE)
}
library(posterior)
library(future)
plan(multisession)
options(SBC.min_chunk_size = 10)
# Setup caching of results
if(use_cmdstanr) {
cache_dir <- "./_rejection_sampling_SBC_cache"
} else {
cache_dir <- "./_rejection_sampling_rstan_SBC_cache"
}
if(!dir.exists(cache_dir)) {
dir.create(cache_dir)
}We’ll use a very simple model throughout this vignette:
data {
int<lower=0> N;
array[N] real y;
}
parameters {
real mu;
}
model {
mu ~ normal(0, 2);
y ~ normal(mu, 1);
}
if(use_cmdstanr) {
backend <- SBC_backend_cmdstan_sample(cmdstan_model("stan/rejection_sampling.stan"), iter_warmup = 800, iter_sampling = 800)
} else {
backend <- SBC_backend_rstan_sample(stan_model("stan/rejection_sampling.stan"), iter = 1600, warmup = 800)
}## In file included from stan/lib/stan_math/lib/boost_1.81.0/boost/multi_array/multi_array_ref.hpp:32,
## from stan/lib/stan_math/lib/boost_1.81.0/boost/multi_array.hpp:34,
## from stan/lib/stan_math/lib/boost_1.81.0/boost/numeric/odeint/algebra/multi_array_algebra.hpp:22,
## from stan/lib/stan_math/lib/boost_1.81.0/boost/numeric/odeint.hpp:63,
## from stan/lib/stan_math/stan/math/prim/functor/ode_rk45.hpp:9,
## from stan/lib/stan_math/stan/math/prim/functor/integrate_ode_rk45.hpp:6,
## from stan/lib/stan_math/stan/math/prim/functor.hpp:16,
## from stan/lib/stan_math/stan/math/rev/fun.hpp:200,
## from stan/lib/stan_math/stan/math/rev.hpp:12,
## from stan/lib/stan_math/stan/math.hpp:19,
## from stan/src/stan/model/model_header.hpp:4,
## from C:/Users/Martin/AppData/Local/Temp/RtmpGUKLZA/model-451c476b1bf3.hpp:2:
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:180:45: warning: 'template<class _Arg, class _Result> struct std::unary_function' is deprecated [-Wdeprecated-declarations]
## 180 | : public boost::functional::detail::unary_function<typename unary_traits<Predicate>::argument_type,bool>
## | ^~~~~~~~~~~~~~## In file included from C:/rtools43/ucrt64/include/c++/13.2.0/string:49,
## from C:/rtools43/ucrt64/include/c++/13.2.0/bits/locale_classes.h:40,
## from C:/rtools43/ucrt64/include/c++/13.2.0/bits/ios_base.h:41,
## from C:/rtools43/ucrt64/include/c++/13.2.0/ios:44,
## from C:/rtools43/ucrt64/include/c++/13.2.0/istream:40,
## from C:/rtools43/ucrt64/include/c++/13.2.0/sstream:40,
## from C:/rtools43/ucrt64/include/c++/13.2.0/complex:45,
## from stan/lib/stan_math/lib/eigen_3.4.0/Eigen/Core:50,
## from stan/lib/stan_math/lib/eigen_3.4.0/Eigen/Dense:1,
## from stan/lib/stan_math/stan/math/prim/fun/Eigen.hpp:22,
## from stan/lib/stan_math/stan/math/rev.hpp:4:
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:117:12: note: declared here
## 117 | struct unary_function
## | ^~~~~~~~~~~~~~## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:214:45: warning: 'template<class _Arg1, class _Arg2, class _Result> struct std::binary_function' is deprecated [-Wdeprecated-declarations]
## 214 | : public boost::functional::detail::binary_function<
## | ^~~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:131:12: note: declared here
## 131 | struct binary_function
## | ^~~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:252:45: warning: 'template<class _Arg, class _Result> struct std::unary_function' is deprecated [-Wdeprecated-declarations]
## 252 | : public boost::functional::detail::unary_function<
## | ^~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:117:12: note: declared here
## 117 | struct unary_function
## | ^~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:299:45: warning: 'template<class _Arg, class _Result> struct std::unary_function' is deprecated [-Wdeprecated-declarations]
## 299 | : public boost::functional::detail::unary_function<
## | ^~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:117:12: note: declared here
## 117 | struct unary_function
## | ^~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:345:57: warning: 'template<class _Arg, class _Result> struct std::unary_function' is deprecated [-Wdeprecated-declarations]
## 345 | class mem_fun_t : public boost::functional::detail::unary_function<T*, S>
## | ^~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:117:12: note: declared here
## 117 | struct unary_function
## | ^~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:361:58: warnin## g: 'template<class _Arg1, class _Arg2, class _Result> struct std::binary_function' is deprecated [-Wdeprecated-declarations]
## 361 | class mem_fun1_t : public boost::functional::detail::binary_function<T*, A, S>
## | ^~~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:131:12: note: declared here
## 131 | struct binary_function
## | ^~~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:377:63: warning: 'template<class _Arg, class _Result> struct std::unary_function' is deprecated [-Wdeprecated-declarations]
## 377 | class const_mem_fun_t : public boost::functional::detail::unary_function<const T*, S>
## | ^~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:117:12: note: declared here
## 117 | struct unary_function
## | ^~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:393:64: warning: 'template<class _Arg1, class _Arg2, class _Result> struct std::binary_function' is deprecated [-Wdeprecated-declarations]
## 393 | class const_mem_fun1_t : public boost::functional::detail::binary_function<const T*, A, S>
## | ^~~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:131:12: note: declared here
## 131 | struct binary_function
## | ^~~~~~~~~~~~~~~## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:438:61: warning: 'template<class _Arg, class _Result> struct std::unary_function' is deprecated [-Wdeprecated-declarations]
## 438 | class mem_fun_ref_t : public boost::functional::detail::unary_function<T&, S>
## | ^~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:117:12: note: declared here
## 117 | struct unary_function
## | ^~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:454:62: warning: 'template<class _Arg1, class _Arg2, class _Result> struct std::binary_function' is deprecated [-Wdeprecated-declarations]
## 454 | class mem_fun1_ref_t : public boost::functional::detail::binary_function<T&, A, S>
## | ^~~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:131:12: note: declared here
## 131 | struct binary_function
## | ^~~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:470:67: warning: 'template<class _Arg, class _Result> struct std::unary_function' is deprecated [-Wdeprecated-declarations]
## 470 | class const_mem_fun_ref_t : public boost::functional::detail::unary_function<const T&, S>
## | ^~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:117:12: note: declared here
## 117 | struct unary_function
## | ^~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:487:68: warning: 'template<class _Arg1, class _Arg2, class _Result> struct std::binary_function' is deprecated [-Wdeprecated-declarations]
## 487 | class const_mem_fun1_ref_t : public boost::functional::detail::binary_function<const T&, A, S>
## | ^~~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bi## ts/stl_function.h:131:12: note: declared here
## 131 | struct binary_function
## | ^~~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:533:73: warning: 'template<class _Arg, class _Result> struct std::unary_function' is deprecated [-Wdeprecated-declarations]
## 533 | class pointer_to_unary_function : public boost::functional::detail::unary_function<Arg,Result>
## | ^~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:117:12: note: declared here
## 117 | struct unary_function
## | ^~~~~~~~~~~~~~
## stan/lib/stan_math/lib/boost_1.81.0/boost/functional.hpp:557:74: warning: 'template<class _Arg1, class _Arg2, class _Result> struct std::binary_function' is deprecated [-Wdeprecated-declarations]
## 557 | class pointer_to_binary_function : public boost::functional::detail::binary_function<Arg1,Arg2,Result>
## | ^~~~~~~~~~~~~~~
## C:/rtools43/ucrt64/include/c++/13.2.0/bits/stl_function.h:131:12: note: declared here
## 131 | struct binary_function
## | ^~~~~~~~~~~~~~~## In file included from stan/lib/stan_math/stan/math/prim/prob/von_mises_lccdf.hpp:5,
## from stan/lib/stan_math/stan/math/prim/prob/von_mises_ccdf_log.hpp:4,
## from stan/lib/stan_math/stan/math/prim/prob.hpp:359,
## from stan/lib/stan_math/stan/math/prim.hpp:16,
## from stan/lib/stan_math/stan/math/rev.hpp:16:
## stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp: In function 'stan::return_type_t<T_x, T_sigma, T_l> stan::math::von_mises_cdf(const T_x&, const T_mu&, const T_k&)':
## stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: '-Wmisleading-indentation' is disabled from this point onwards, since column-tracking was disabled due to the size of the code/headers
## 194 | if (cdf_n < 0.0)
## |## stan/lib/stan_math/stan/math/prim/prob/von_mises_cdf.hpp:194: note: adding '-flarge-source-files' will allow for more column-tracking support, at the expense of compilation time and memoryNo rejections
First, we’ll use a generator that matches the model exactly.
N <- 10
generator <- SBC_generator_function(function() {
mu <- rnorm(1, 0, 2)
list(
variables = list(mu = mu),
generated = list(N = N, y = rnorm(N, mu, 1))
)
})So we expect the SBC to pass even with a large number of fits.
set.seed(2323455)
datasets <- generate_datasets(generator, 1000)
results <- compute_SBC(datasets, backend, keep_fits = FALSE,
cache_mode = "results",
cache_location = file.path(cache_dir, "no_rejections"))## Results loaded from cache file 'no_rejections'## - 2 (0%) fits had at least one Rhat > 1.01. Largest Rhat was 1.012.## Not all diagnostics are OK.
## You can learn more by inspecting $default_diagnostics, $backend_diagnostics
## and/or investigating $outputs/$messages/$warnings for detailed output from the backend.
plot_ecdf_diff(results)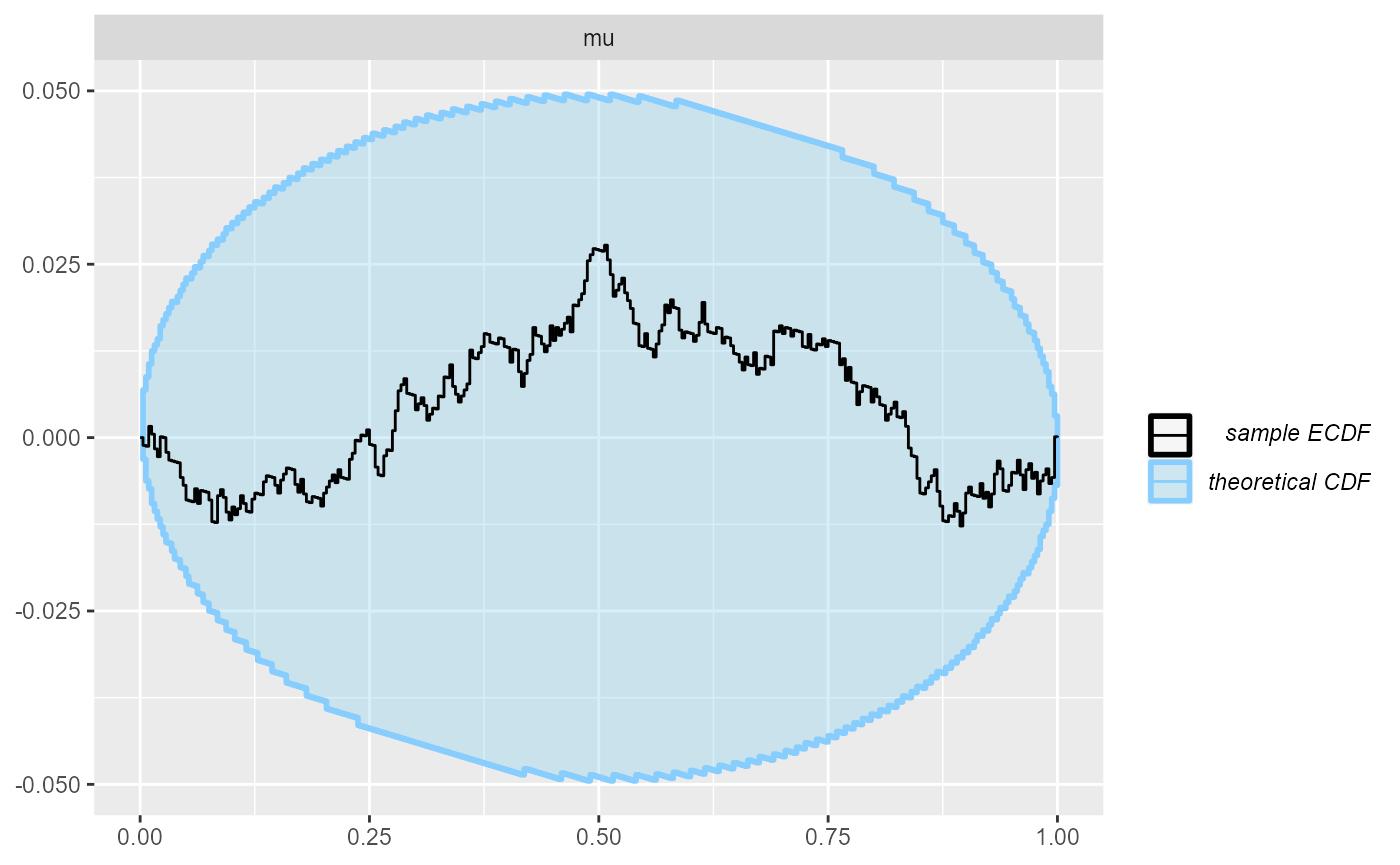
plot_rank_hist(results)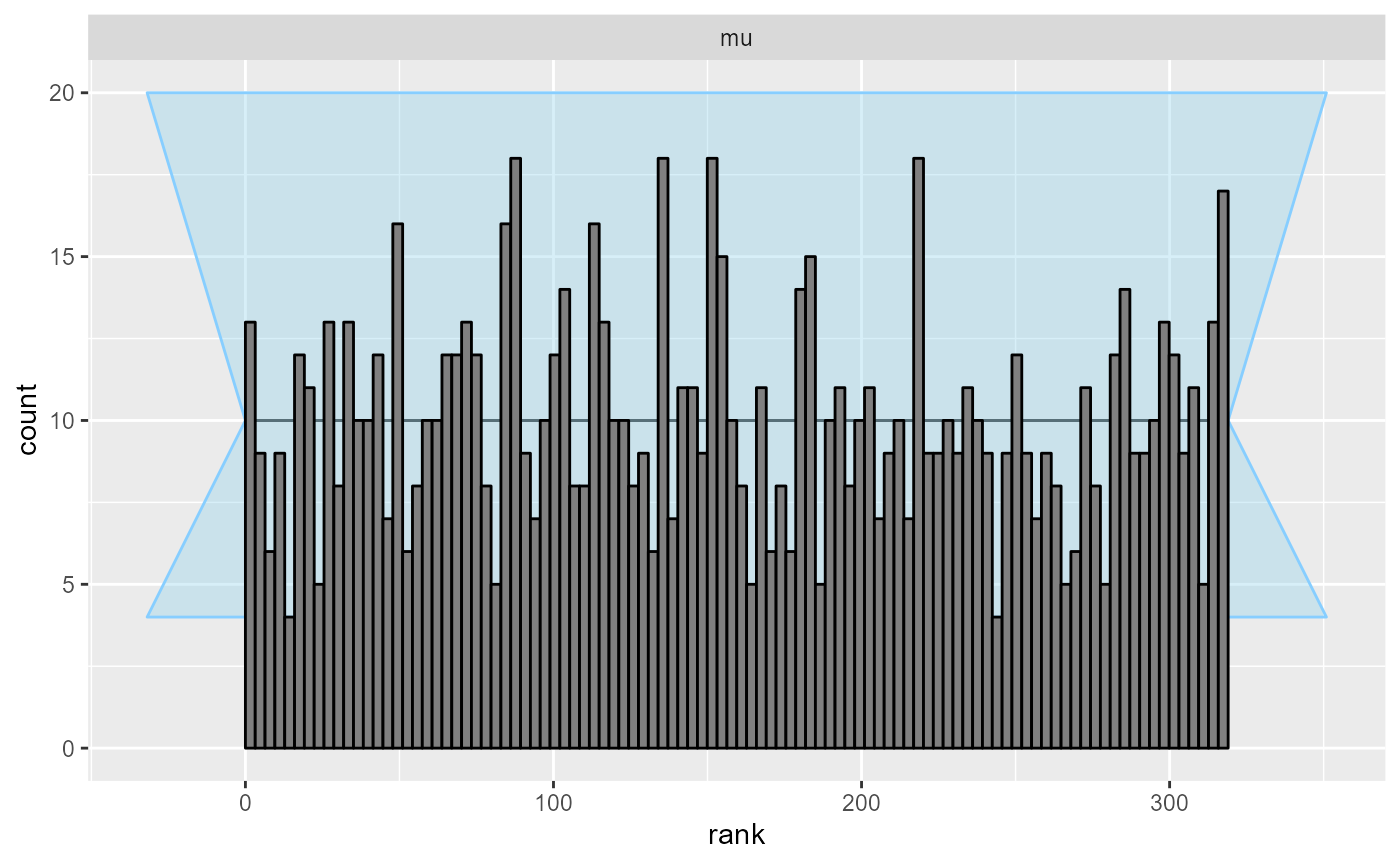
Indeed, all looks good.
Rejection based on unobserved variables
Now let us modify the generator to reject based on values of an unobserved variable.
generator_reject_unobserved <- SBC_generator_function(function() {
repeat {
mu <- rnorm(1, 0, 2)
if(mu > 3) {
break
}
}
list(
variables = list(mu = mu),
generated = list(N = N, y = rnorm(N, mu, 1))
)
})We don’t even need to run very many fits to see the problem.
set.seed(21455)
datasets_reject_unobserved <- generate_datasets(generator_reject_unobserved, 200)
results_reject_unobserved <- compute_SBC(datasets_reject_unobserved, backend, keep_fits = FALSE,
cache_mode = "results",
cache_location = file.path(cache_dir, "reject_unobserved"))## Results loaded from cache file 'reject_unobserved'## - 1 (0%) fits had at least one Rhat > 1.01. Largest Rhat was 1.011.## Not all diagnostics are OK.
## You can learn more by inspecting $default_diagnostics, $backend_diagnostics
## and/or investigating $outputs/$messages/$warnings for detailed output from the backend.
plot_ecdf_diff(results_reject_unobserved)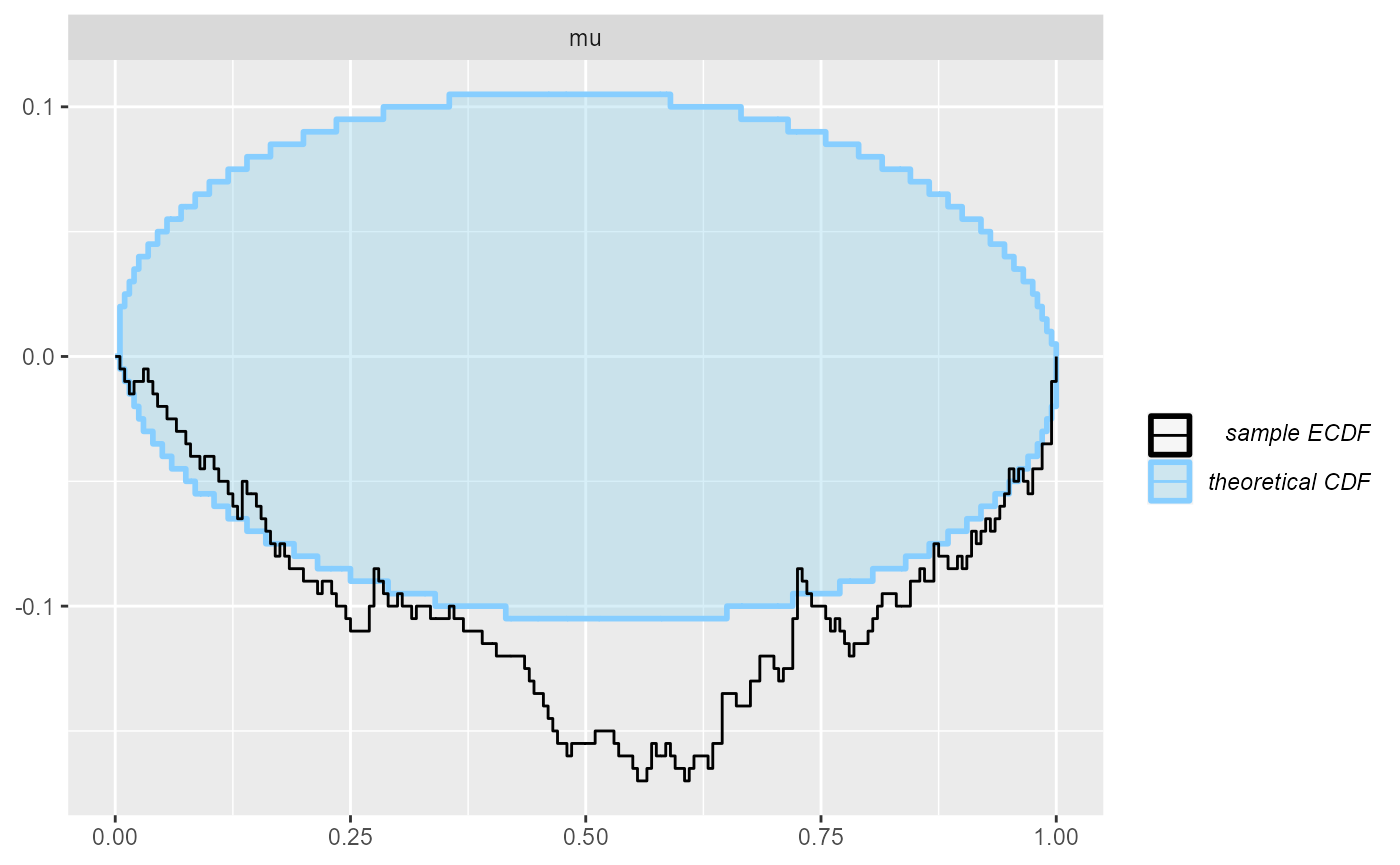
plot_rank_hist(results_reject_unobserved)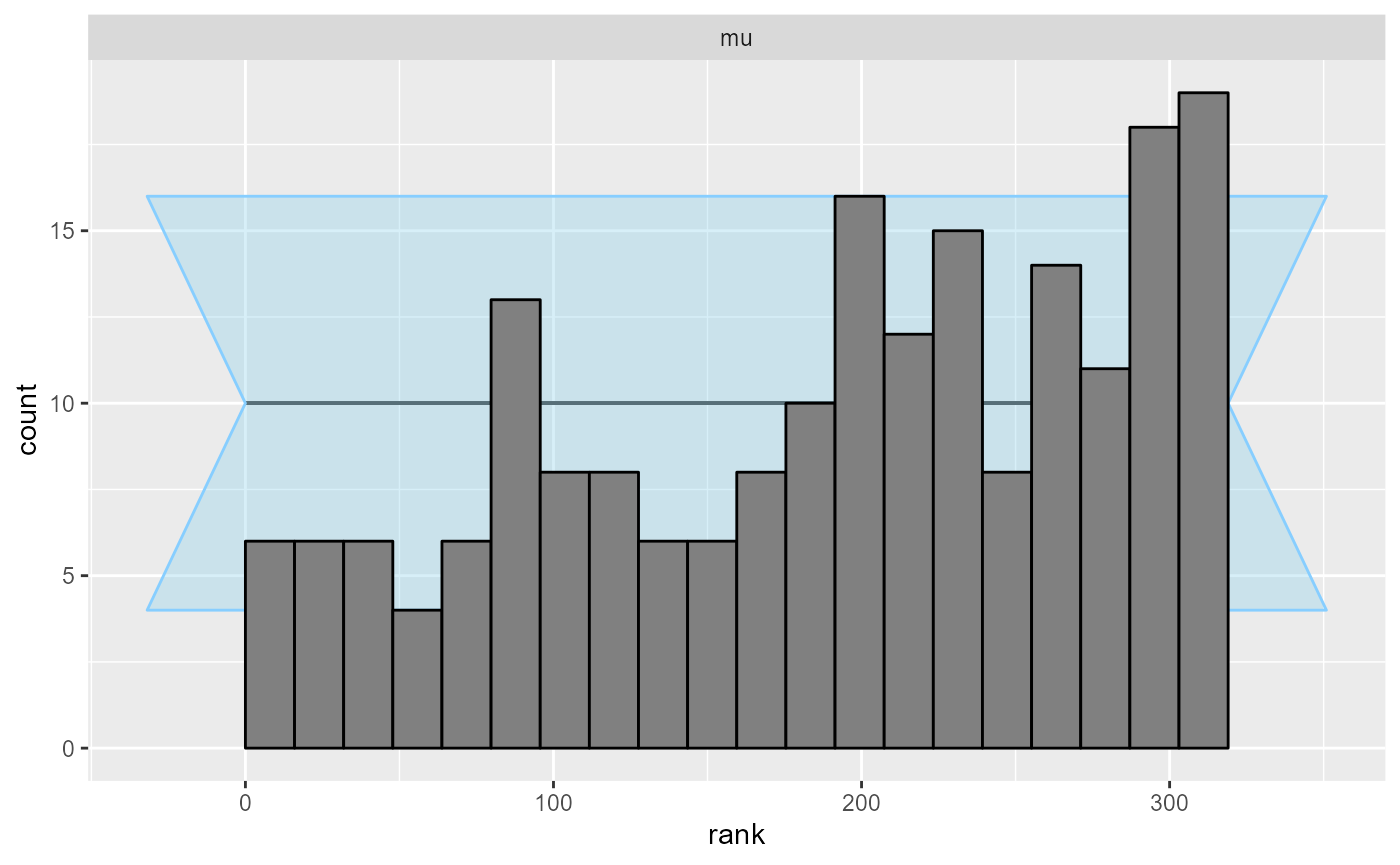
Indeed, we see a clear failure.
Rejecting based on data
But what if we reject based on the values of data? This should in theory result in just a constant change in posterior density and not affect SBC. (SBC will however then check only the non-rejected parts of the data space). We will do a relatively aggressive rejection scheme (reject more than 50% of simulations).
generator_reject_y <- SBC_generator_function(function() {
repeat {
mu <- rnorm(1, 0, 2)
y <- rnorm(N, mu, 1)
if(mean(y) > 5) {
break
}
}
list(
variables = list(mu = mu),
generated = list(N = N, y = y)
)
})
set.seed(369654)
datasets_reject_y <- generate_datasets(generator_reject_y, 1000)
results_reject_y <- compute_SBC(datasets_reject_y, backend, keep_fits = FALSE,
cache_mode = "results",
cache_location = file.path(cache_dir, "reject_y"))## Results loaded from cache file 'reject_y'## - 1 (0%) fits had at least one Rhat > 1.01. Largest Rhat was 1.01.## Not all diagnostics are OK.
## You can learn more by inspecting $default_diagnostics, $backend_diagnostics
## and/or investigating $outputs/$messages/$warnings for detailed output from the backend.
plot_rank_hist(results_reject_y)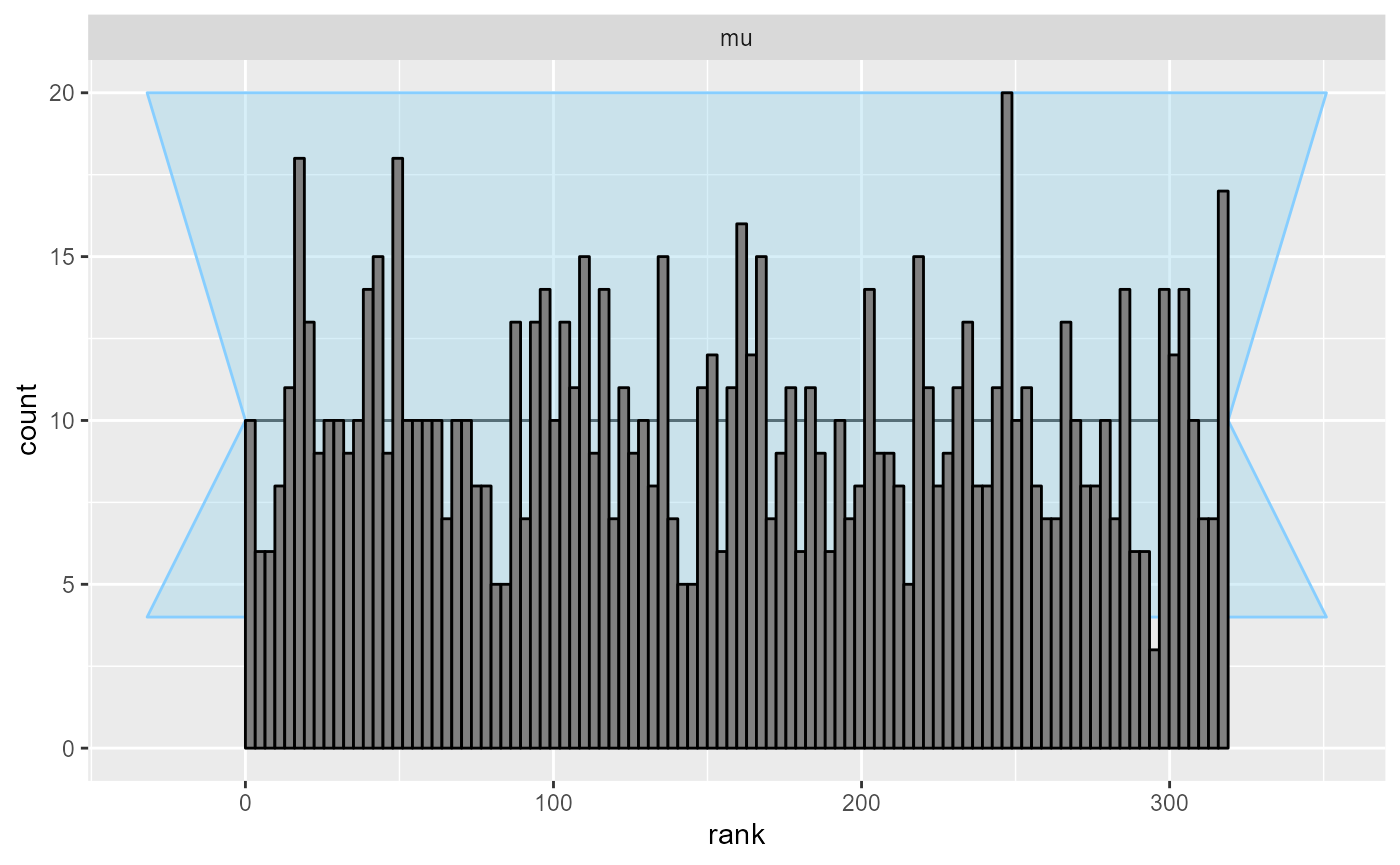
plot_ecdf_diff(results_reject_y)
We see that even with quite heavy rejection based on y, SBC to a high resolution passes.
Take home message
If our priors can sometimes result in simulated data that is unrealistic, but we are unable to specify a better prior directly (e.g. because we would need to define some sort of joint prior), we can use rejection sampling to prune unrealistic simulations as long as we only filter by the observed data and don’t directly use any unobserved variable values. Notably, filtering based on divergences or other fitting issues is also just a function of data and thus permissible. The resulting SBC will however provide guarantees only for data that would not be rejected by the same criteria.