A backend that just calls a function.

If the function returns a draws_matrix object, no other work is necessary to make it work with SBC.

SBC_backend_function(
  func,
  generated_arg = "generated",
  cores_arg = NULL,
  args = list(),
  iid_draws = FALSE,
  default_thin_ranks = 10
)

Arguments

func

the function that will be called in SBC_fit()

generated_arg

name of the argument of func that will receive the generated data. If NULL, data is not passed to the function.

cores_arg

name of the argument of func that will receive the number of cores to use. If NULL, information on cores is not passed.

args

a (named) list of additional arguments to the function

iid_draws

does the result of the backend have independent identically distribute draws (will be returned by SBC_backend_iid_draws() for this backend).

default_thin_ranks

suggested thinning if user does not specify any (will be returned by SBC_backend_default_thin_ranks() for this backend).

Examples

# Generate t-distributed variables as a ratio of standard normal (z)
# and transformed chi-squared (v) variables.
# What is the conditional distribution of z if t is observed?
# See https://math.stackexchange.com/a/5085538/423833 for derivation that it
# is generalized gamma distribution. Here we test this is correct.

N_sims <- 100
df <- 5
z <- rnorm(N_sims)
v <- rchisq(N_sims, df = df)
t <- z / sqrt(v/df)

# Bundle in a dataset with extra quantities
my_data <- SBC_datasets(
  variables = posterior::draws_matrix
  (z = z, v = v, lik = abs(z) * dchisq(df * z^2 / t^2, df = df)),
  generated = purrr::map(t, \(t) list(t = t, df = df)))

# Main workhorse function
my_post_func <- function(generated) {
  df <- generated$df
  t <- generated$t
  gg_d <- df + 1
  gg_p <- 2
  gg_a <- 1/sqrt(df/(2*t^2) + 0.5)

  # Transform to parametrization used by ggamma
  gg_b <- gg_p
  gg_k <- gg_d / gg_p

  abs_z <- ggamma::rggamma(1000, gg_a, gg_b, gg_k)
  v <- df * abs_z^2 / t^2
  lik = abs_z * dchisq(df * abs_z^2 / t^2, df = df)
  posterior::draws_matrix(z = abs_z * sign(generated$t),
                          v = v,
                          lik = lik)
}

backend <- SBC_backend_function(my_post_func, iid_draws = TRUE)
res <- compute_SBC(my_data, backend, keep_fits = FALSE)

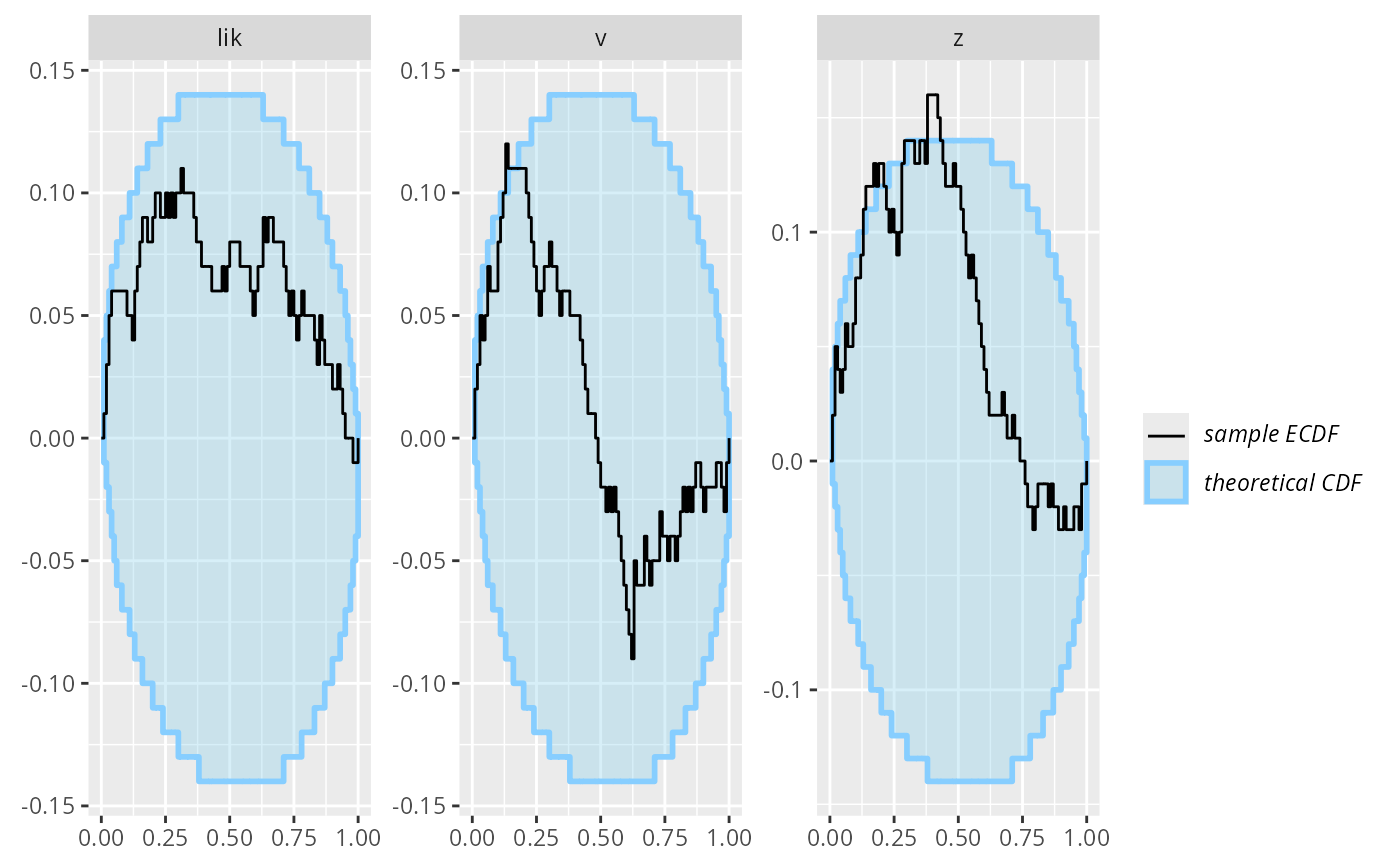
plot_ecdf_diff(res)

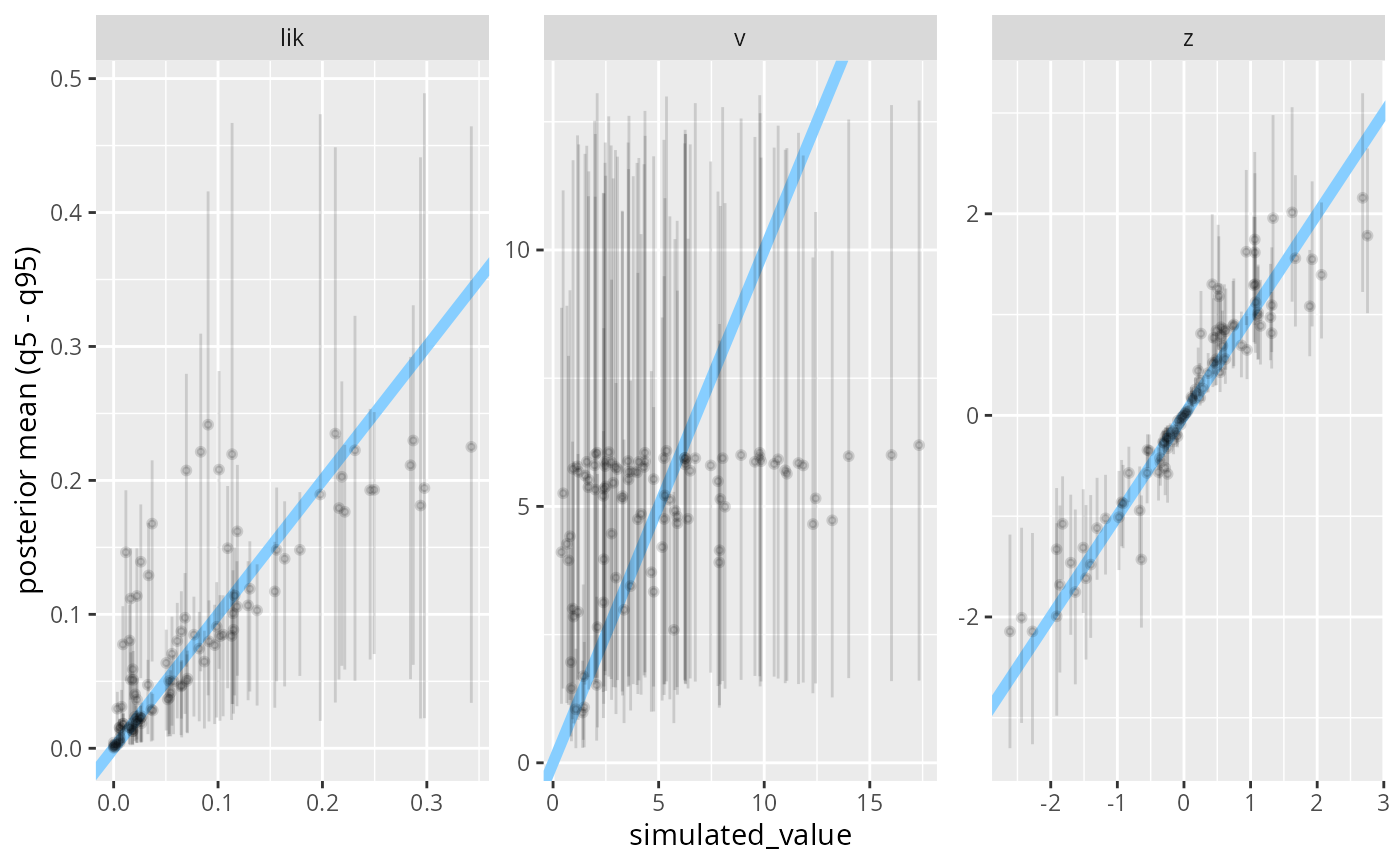
plot_sim_estimated(res)